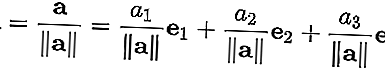يمكن تعريف المتجه في الرياضيات والفيزياء على أنه كائنات هندسية لها المقدار والاتجاه. يتم تصوير المتجه بسهم ، حيث تُظهر قاعدة السهم نقطة التقاط (نقطة بداية) للمتجه ، ويشير طول السهم إلى حجم أو قيمة المتجه (كلما زاد طول السهم ، زادت قيمة أو قيمة المتجه ، والعكس صحيح) ، بينما يشير السهم إلى اتجاه المتجه.
في الكتابة ، إذا بدأ المتجه عند النقطة A وينتهي عند النقطة B ، فيمكن كتابته بحرف صغير يوجد فوقه خط / سهم مثل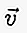 
أو 
أو 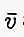أيضًا:
أنواع النواقل
ينقسم المتجه في الرياضيات إلى 4 أنواع ، بما في ذلك:
ناقل الموقف
متجه تكون نقطة بدايته عند 0 (0،0) ونهايته A (a1، a2).
ناقل صفر
"المتجه صفر" ( متجه فارغ أو متجه صفري ) متجه طوله "صفر". الكتابة في إحداثيات هذا المتجه هي (0،0،0) ، وعادة ما يُعطى الرمز 
، أو 0 . يختلف هذا المتجه عن المتجهات الأخرى في أنه لا يمكن تطبيعه (أي ، لا يوجد متجه وحدة هو مضاعف لمتجه الصفر) مجموع المتجهات الصفرية مع أي متجه a هو a (أي 0 + a = a ).
متجه الصفر ليس له اتجاه متجه واضح.
حتى النصر
هو متجه بطول "واحد". عادة ما تستخدم نواقل الوحدة فقط للإشارة إلى الاتجاه. يمكن قسمة المتجه بأي طول على الطول للحصول على متجه الوحدة. يُعرف هذا باسم "تطبيع" المتجه. غالبًا ما يُشار إلى متجه الوحدة بواسطة "قبعة" فوق الحرف الصغير "a" كما هو الحال في - .
لتسوية المتجه a = [ a 1 ، a 2 ، a 3 ] ، قسّم المتجه على طوله || أ ||. وبالتالي:
ناقل القاعدة
متجه وحدة عمودي على بعضها البعض. في متجه الفضاء ثنائي الأبعاد ( R 2 ) له متجهان أساسيان ، وهما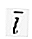 
= (1 ، 0) و 
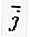= (0 ، 1).
تشابه اثنين من النواقل
يقال أن متجهين متماثلان إذا كان لهما نفس الطول والاتجاه
محاذاة متجهين
يطلق على متجهين متوازيين (متوازيين) إذا كان الخط الذي يمثل المتجهين متوازيين.
عمليات ناقلات
الضرب القياسي
يمكن ضرب المتجه بواسطة عددي ينتج عنه متجه أيضًا ، والمتجه الناتج هو:
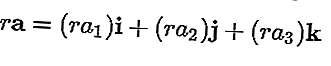
جمع المتجهات والطرح المتجه
على سبيل المثال، وناقلات و = و 1 ط + ل 2 ي + على 3 ك و ب = ب 1 ط + ب 2 ي + ب 3 ك
نتيجة a زائد b هي: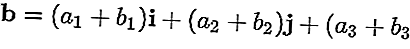 
ينطبق تقليل الاتجاه أيضًا عن طريق استبدال علامة + بعلامة -
