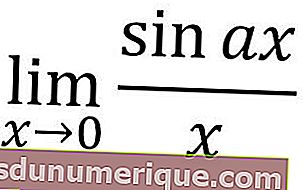يتم تعريف حد دالة حساب المثلثات على أنه أقرب قيمة لزاوية في دالة حساب المثلثات. يمكن استبدال هذا الحساب مثل حد الدالة الجبرية ، ولكن بدالة مثلثية يجب تغييرها أولاً.
يجب تحويل الدالة المثلثية إلى متطابقة مثلثية لحد غير محدد ، وهو حد ، إذا تم استبداله ، سيكون 0. بالإضافة إلى ذلك ، هناك أيضًا طريقة لحساب حد غير محدد دون استخدام المتطابقة المثلثية ، ولكن باستخدام نظرية النهاية المثلثية. يستخدم البعض الآخر كلاً من الهوية والنظرية في وقت واحد.
لتحديد القيمة الحدية للوظائف المثلثية ، هناك طرق مختلفة يمكن استخدامها ، وهي الطرق العددية ، والتعويض ، والعوملة ، وأوقات الأقران ، والمشتقات.
(اقرأ أيضًا: قياس الرؤية باستخدام الصيغ المثلثية)
ولكن بناءً على القيمة ، يمكننا تقسيم هذه الصيغة إلى نسختين ، أي تلك القريبة من العدد والقريبة من الصفر.
X تقترب من رقم
إذا كان لدينا حد الدالة المثلثية التي تقترب x من الرقم c ، فيمكننا تحديد قيمتها بالتعويض عن c في دالة المثلث. الصيغ كالتالي.

X تقترب من الصفر
إذا اقترب x من نهاية دالة مثلثية من الصفر ، فيمكننا استخدام الصيغ أدناه.

إذا كان الشكل غير المحدد بعد استبدال قيمة x في دالة المثلث هو 0/0 ∞ / ، فعندئذٍ لتحديد القيمة الحدية للدالة المثلثية ، يمكنك استخدام قاعدة L'Hospital ، وهي
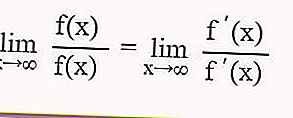
فهم الحدس لحدود وظائف Trig
إن الفهم الحدسي لحدود الدالة المثلثية هو نفس حد الدالة الجبرية. يوجد حد الدالة المثلثية إذا وفقط إذا كان الحد الأيسر والحد الأيمن موجودًا وكان الحد الأيسر مساويًا للحد الأيمن.