الدائرة هي مجموعة من النقاط التي تكون على مسافة متساوية من نقطة. يتم تحديد إحداثيات هذه النقاط بترتيب المعادلات الدائرية. يتم تحديد ذلك بناءً على طول نصف القطر وإحداثيات مركز الدائرة.
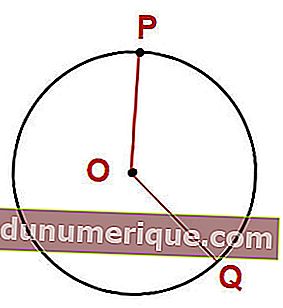
في الصورة أعلاه ، يمكننا أن نستنتج أن OP = OQ. تسمى النقطة O بمركز الدائرة ، بينما OP و OQ هما نصف القطر. دعونا نتأمل المثال التالي.
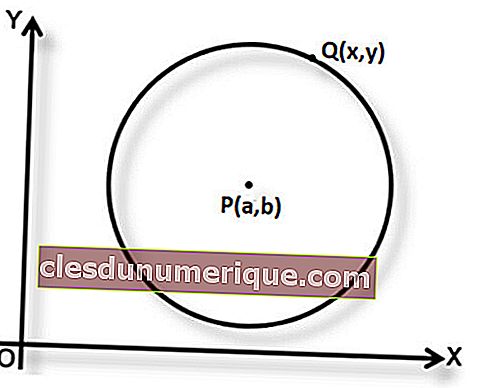
P (a، b) هي مركز الدائرة وطول نصف القطر r. إذا كانت Q (x ، y) هي نقطة تقع على الدائرة ، بناءً على تعريف الدائرة ، يمكن استنتاج أن PQ = r. من هذا ، يمكننا صياغة معادلة الدائرة حيث يكون المركز P (a، b) و r هو نصف القطر.
√ (س - أ) 2 + (ص - ب) 2 = ص
(س - أ) 2 + (ص - ب) 2 = r2
دعنا نعمل على مثال مشكلة أدناه.
أوجد معادلة الدائرة التي يقع مركزها عند النقطة (-5،4) التي نصف قطرها 7!
من هذه العبارات ، نعلم أن a = -5 ، و b = 4 ، و r = 7. إذا عوضنا بها في المعادلة ، نحصل على الإجابة التالية.
(س - (-5)) 2 + (ص - 4) 2 = 72
(س + 5) 2 + (ص - 4) 2 = 49
ماذا عن الدائرة التي يكون مركزها عند P (0،0)؟ معادلة الدائرة على النحو التالي.
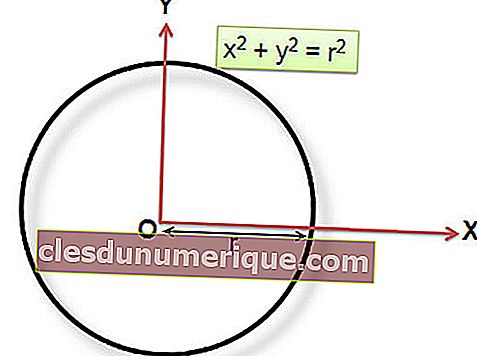
يمكن التعبير عن الشكل العام للمعادلة الدائرية في الأشكال التالية.
(س - أ) 2 + (ص - ب) 2 = r2 ، أو
X2 + y2 - 2ax - 2by + a2 + b2 - r2 = 0 ، أو
X2 + y2 + Px + Qy + S = 0 ، حيث P = -2a و Q = -2b و S = a2 + b2 - r2
شروط تحديد معادلة الدائرة
تحتوي المعادلة الدائرية على ثلاثة متغيرات عشوائية. يمكن تحديد معادلة الدائرة إذا كانت قيم المتغيرات الثلاثة معروفة. لمعرفة قيم هذه المتغيرات الثلاثة ، يجب استيفاء أحد الشروط التالية:
- إحداثيات النقاط الثلاث على الدائرة معروفة.
- تُعرف إحداثيات نقطتين على الدائرة المتصلة بقطر الدائرة.
- إحداثيات النقطة المركزية وإحداثيات النقطة على الدائرة معروفة.