إذا كنت تدرس الرياضيات ، فلا بد أنك سمعت أو درست علم المثلثات. حسنًا ، علم المثلثات هو فرع من فروع الرياضيات يدرس العلاقة بين الزوايا وأطوال أضلاع المثلثات ، مثل الجيب وجيب التمام والظل. إذا أخذنا علم المثلثات حرفيًا ، فهو مشتق من اليونانية ، أي تريغونون الذي يعني "الزوايا الثلاث" والمترون ، وهو ما يعني "القياس". كما هو الحال مع المواد المختلفة في الرياضيات ، هناك صيغ مثلثية تحتاج إلى معرفتها.
في هذه المناسبة ، سنحاول فهم أنواع مختلفة من الصيغ وأيضًا أمثلة لمشاكلهم.
الصيغ المثلثية
يعتبر مفهوم علم المثلثات مفهومًا مهمًا في المثلثات. تتم صياغة القيم المثلثية بناءً على نسبة أضلاع المثلث القائم. هناك ست قيم نسبة مثلثية ، وهي الجيب (الخطيئة) وجيب التمام (جيب التمام) والظل (الظل) وقاطع التمام (التمام) والقاطع (ثانية) والظل التمام (cot). يمكن تحديد هذه الأنواع الستة من القيم المثلثية بمقارنة أطوال الأضلاع بقواعد معينة.
تتعدد استخدامات علم المثلثات ، بدءًا من علم الفلك والجغرافيا ونظرية الموسيقى والصوتيات وتحليل السوق المالي البصري والإلكترونيات ونظرية الاحتمالات والإحصاء وعلم الأحياء والتصوير الطبي والصيدلة والكيمياء وغيرها الكثير.
حان الوقت الآن للتعرف على الصيغ المثلثية المختلفة في هذا الدرس.
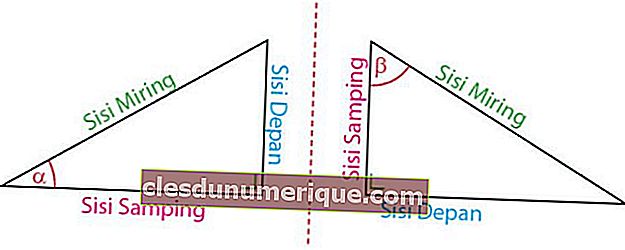
مصدر الصورة: idschool.net
بناءً على موقعه على الزاوية ، يتم تقسيم جوانب المثلث - الكوع إلى ثلاثة أنواع ، وهي الجانب الأمامي والجانب الجانبي والوتر. الجانب الأمامي هو الجانب المواجه للزاوية. الجانب على جانب الزاوية. يكون الجانب المائل دائمًا أمام الزاوية 90 درجة.
حسنًا ، الدوال المثلثية الرئيسية الثلاث هي الدوال الجيب وجيب التمام والظل. يمكن رؤية تعريف الوظائف الثلاث بناءً على جوانب وزوايا المثلث القائم في الشكل والمعادلة أدناه.
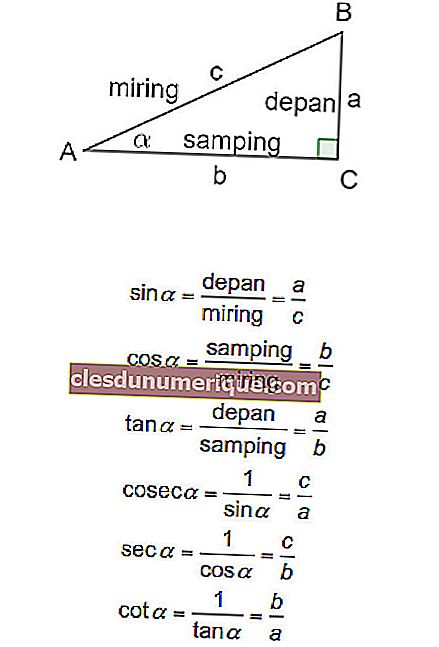
الآن ، على وجه التحديد بالنسبة للزوايا الخاصة ، تكون القيم المثلثية كما يلي:
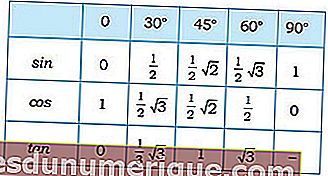
مصدر الصورة: madematics.net
مقارنة الزاوية المثلثية المترابطة
النسبة المثلثية للزاوية ذات الصلة هي امتداد لقيمة المثلث الأساسية التي يتم تحديدها من زاوية المثلث القائم. تقع زاوية المثلث الأيمن في الربع الأول فقط لأنها زاوية حادة حجمها 0 ° - 90 °.
الزاوية المركزية للدائرة ما بين 0 ° - 360 °. الزاوية مقسمة إلى أربعة أرباع ، كل ربع له نطاق 90 درجة.
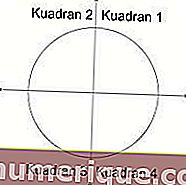
مصدر الصورة: studiobelajar.com
- الربع 1 له زاوية بين 0 ° - 90 °. جميع قيم النسبة المثلثية موجبة في هذا الربع.
- الربع 2 له زاوية بين 90 درجة - 180 درجة. في هذا الربع ، تكون قيم الجيب وقاطع التمام موجبة فقط.
- الربع 3 له زاوية بين 180 درجة - 270 درجة. في هذا الربع ، تكون الظلال والمظلات موجبة فقط.
- الربع 4 له زاوية بين 270 درجة - 360 درجة. في هذا الربع ، يكون جيب التمام والقطع موجبين فقط.
الهوية المثلثية
نظرية فيثاغورس ، أي a2 + b2 = c2 ، هي أساس تحضير الهويات المثلثية. تعبر المتطابقات المثلثية عن علاقة الدالة المثلثية بالدوال المثلثية الأخرى.
مجموع الجيب والجيب التربيعي يساوي واحدًا. إذا تم تقسيم كلا الجانبين على مربع جيب التمام ، فإن واحدًا زائد مربع الظل يساوي مربع القاطع. وبالمثل ، إذا تم تقسيم كلا الجانبين على مربع الجيب ، فيمكننا الحصول على واحد زائد ظل التمام يساوي مربع جيب التمام.
ها هي صيغة الهوية:
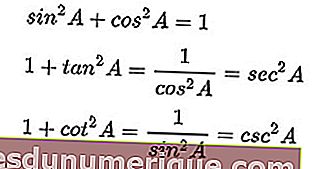
مصدر الصورة: wikipedia.org
صيغ أخرى مختلفة
هناك صيغة أخرى يجب أن تعرفها وهي:
صيغة مجموع الزوايا واختلافها:
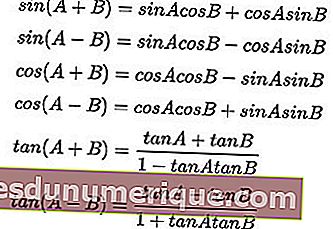
صيغ الضرب المثلثية:
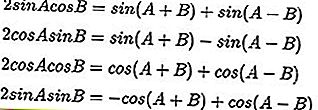
معادلات الجمع والاختلاف المثلثية:
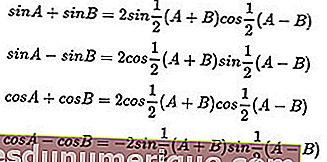
أمثلة على مشاكل Trig
أوجد قيمة 2 cos 75 ° cos 15 °:
المحلول:
بناءً على المعلومات الموجودة في المشكلة ، يمكننا أن نرى أن المشكلة المذكورة أعلاه تتضمن الضرب المثلثي. استخدم صيغة الضرب لجيوب التمام الموصوفة أعلاه ، وهي 2 جتا أ + جتا ب = جتا (أ + ب) + جتا (أ - ب).
إجابة:
2 cos 75 ° cos 15 ° = cos (75 +15) ° + cos (75-15) °
= cos 90 درجة + cos 60 درجة
= 0 +
= ½
هذه مجموعة من الصيغ والمشكلات المثلثية التي يمكنك تعلمها وفهمها. لكي تتمكن من فهمها بشكل أفضل ، يمكنك تجربة PROBLEM ، وهو حل مرجح وكامل عبر الإنترنت لممارسة الأسئلة وفقًا لأحدث المناهج في Smart Class. بدءاً من المرحلة الابتدائية والإعدادية وحتى الثانوية مع مواد مختلفة مثل الرياضيات والفيزياء والكيمياء وغيرها. هنا يمكنك تعلم أنواع مختلفة من الصيغ كاملة مع أمثلة على المشاكل ،
هيا، ماذا تنتظرون! لنجرب تمارين PROBLEM في Smart Class الآن.