فقط لكي تعرف ، العلاقات موجودة أيضًا في الرياضيات ، كما تعلم. توجد العلاقات في المادة المتعلقة بالمجموعات. العلاقات هي قواعد تربط أعضاء المجموعة بأعضاء آخرين في المجموعة. العلاقة من المجموعة "أ" إلى المجموعة "ب" تربط أعضاء المجموعة "أ" بأعضاء المجموعة "ب". في هذه الفرصة سوف نتعرف على أمثلة للعلاقات وخصائصها ، بالإضافة إلى أمثلة متنوعة من المشكلات التي يمكن أن تساعدك على فهم هذه المادة بشكل أفضل.
أمثلة على العلاقات وطبيعتها
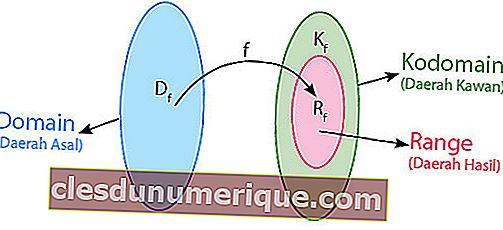
يمكن تعريف العلاقة كقاعدة تربط أعضاء منطقة المنشأ (المجال) وأعضاء المنطقة الصديقة (المجال المشترك). في العلاقة ، لا توجد قواعد خاصة يجب الوفاء بها لمطابقة أعضاء الاتحاد الإقليمي مع أعضاء المناطق الصديقة.
المصدر: idschool.net
يمكن أن يكون لكل عضو في الاتحاد الإقليمي للمنشأ أكثر من شريك واحد أو قد لا يكون لديه شريك على الإطلاق. يمكن التعبير عن علاقة مجموعتين بثلاث طرق ، وهي:
- مخطط السهم
- رسم ديكارتي.
- مجموعة الأزواج المتتالية
فيما يلي شرح إضافي للطرق الثلاث:
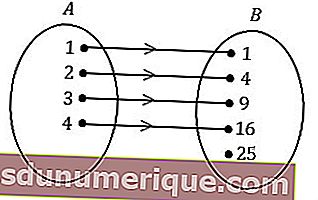
مخططات الأسهم
مخططات الأسهم هي أسهل طريقة للتعبير عن علاقة. سيشكل هذا الرسم البياني نمطًا لعلاقة في شكل سهم يوضح العلاقة من أعضاء المجموعة أ إلى أعضاء المجموعة ب.
المصدر: maretong.com
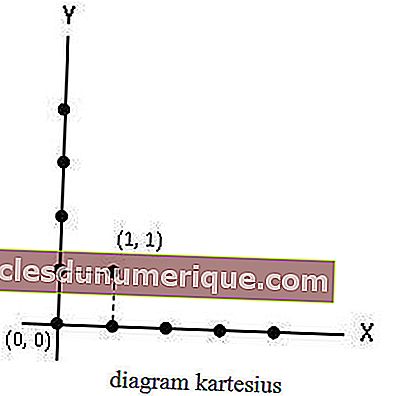
رسم ديكارتي
الرسم التخطيطي الديكارتي هو رسم بياني يتكون من محور X ومحور Y. في الرسم التخطيطي الديكارتي ، توجد أعضاء المجموعة A على المحور X ، بينما توجد أعضاء المجموعة B على المحور Y. والعلاقات التي تربط المجموعة A بـ B يشار إليها بالنقاط أو النقاط.
مجموعة أزواج متتالية
يمكن تمثيل العلاقة التي تربط مجموعة بمجموعة أخرى في شكل مجموعة من الأزواج المرتبة. طريقة الكتابة هي أن أعضاء المجموعة أ يكتبون أولاً ، بينما أعضاء المجموعة ب وهم الأزواج يكتبون في المرتبة الثانية.
أمثلة مثل هذا:
أ = مجموعة العالم ، اليابان ، كوريا ، فرنسا
المجموعة ب = طوكيو ، باريس ، جاكرتا ، سيول
حدد مجموعة الأزواج المرتبة حسب الدولة ورأس المال.
إجابة:
{(العالم ، جاكرتا) ، (اليابان ، طوكيو) ، (كوريا ، سيول) ، (فرنسا ، باريس)}
وظيفة
الوظيفة أو التعيين هو علاقة خاصة من المجموعة أ إلى المجموعة ب ، مع القاعدة التي تنص على أن كل عضو في المجموعة أ يتطابق تمامًا مع عضو المجموعة ب.
ويطلق على نتيجة تعيين من مجال إلى مجال و ظيفة مجموعة أو منطقة النتيجة. كما هو الحال مع العلاقات ، يمكن أيضًا تمثيل الوظائف في شكل مخططات سهم وأزواج مرتبة ومخططات ديكارتية.
المصدر: rumushitung.com
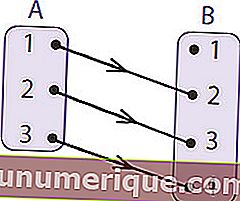
لفهمها أكثر ، انظر إلى الصورة أعلاه. المجموعة أ أو منطقة المنشأ تسمى المجال. المجموعة ب التي هي منطقة صديق تسمى المجال المشترك. يسمى عضو المنطقة المألوفة الناتج عن التعيين منطقة العائد أو نطاق الوظائف. لذلك من مخطط السهم أعلاه يمكن استنتاج ذلك
- المجال (D f) هو A = {1،2،3}
- Codomain هو B = {1،2،3،4}
- المدى / النتيجة (R f) = {2،3،4}
يمكن الإشارة إلى الوظائف بأحرف صغيرة مثل f و g و h و i وما إلى ذلك. تم تعيين وظيفة f الخرائط A لتعيين B ، ثم يمكن الإشارة إليها بواسطة f (x): A → B.
مثال على ذلك هو الوظيفة f التي تعين A إلى B مع القاعدة f: x → 2x + 2. من تدوين الوظيفة ، x هي عضو في المجال. تعني الوظيفة x → 2x + 2 أن الوظيفة f تعين x على 2x + 2. إذن مساحة x بالدالة f هي 2x + 2. لذا يمكنك الإشارة إليها لتكون f (x) = 2x +2.
إذا كانت الدالة f: x → ax + b مع x عضوًا في المجال f ، فإن صيغة الدالة f هي
و (س) = الفأس + ب
مثال على المشاكل:
بالنظر إلى الدالة f: x → 2x - 2 حيث x عدد صحيح. حاول تحديد قيمة f (3).
المحلول:
يمكن تمثيل الوظيفة f: x → 2x - 2 بواسطة f (x) = 2x - 2
وبالتالي،
و (س) = 2 س - 2
و (3) = 2 (3) - 2 = 4
هذا مثال على العلاقات والوظائف في الرياضيات. هل لديك أي أسئلة حول هذا؟ يرجى كتابة سؤالك في عمود التعليقات ، ولا تنس مشاركة هذه المعرفة.