هل تنتبه إذا كان سقف المنزل والخيمة متماثلان تقريبًا؟ إذا نظرت مرة أخرى ، يبدو أنها تتكون من مثلثين في كل طرف ، ثم تغطيتها ببطانية مستطيلة الشكل. يُعرف هذا الشكل أيضًا باسم المنشور الثلاثي. يطلق عليه ذلك لأن القاعدة والغطاء مثلثان. في الهندسة ، سوف ندرس تعريف وصيغة المنشور الثلاثي. في هذه المناسبة ، سنناقش أيضًا أمثلة مختلفة للمشكلة حتى نتمكن من فهم هذه المادة بشكل أكبر.
المنشور هو شكل له غطاء وقاعدة بشكل متطابق من جانبين ، بينما جوانبها الرأسية مستطيلة.
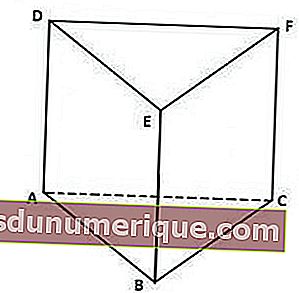
المناشير المثلثة لها الخصائص التالية:
لها قاعدة وغطاء مثلثة متطابقة.
من الصورة أعلاه ، غطاء المنشور ، أي مثلث DEF ، له نفس شكل وحجم المثلث ABC كقاعدته.
المستطيل كجانب عمودي.
يمكنك أن ترى أن المنشور أعلاه محدود بثلاثة مستطيلات على كل جانب من الرأسي ، وهي مستطيلات ACFD و BCFE و ABED.
لها 5 جوانب و 9 حواف و 6 رؤوس.
تتكون الجوانب الخمسة للمنشور الثلاثي من جانب واحد للقاعدة وجانب واحد للغطاء و 3 جوانب رأسية. بينما تتكون الضلوع التسعة من 3 أضلاع عمودية ، و 3 جوانب للقاعدة ، و 3 جوانب من الغطاء. أيضًا ، الرؤوس الستة هي النقاط A و B و C و D و E و F.
الآن ، بعد أن عرفنا خصائص ومعنى المنشور الثلاثي ، حان الوقت للتعرف على صيغ المنشور المثلث وأمثلة لمشاكلها.
الصيغ المنشورية المثلثية ومشاكل الأمثلة
سيكون هناك نوعان من صيغ المنشور الثلاثي التي نتعلمها. صيغة إيجاد الحجم وصيغة إيجاد مساحة السطح. الصيغ كالتالي:
الصوت
بالنسبة للحجم ، سوف نستخدم الصيغة:
V = مساحة القاعدة × الارتفاع
أو
V = (½ x a x h) × ارتفاع المنشور
لذا ، لفهم هذا بشكل أفضل ، دعنا نلقي نظرة على مثال لهذه المشكلة الواحدة:
يبلغ ارتفاع المنشور 10 سم. تتخذ قاعدة المنشور شكل مثلث قائم أطوال أضلاعه 4 سم و 3 سم على التوالي. ما هو حجم هذا المنشور الثلاثي؟
المحلول:
هنا ، نحتاج فقط إلى إدخال الأرقام المعروفة في صيغة مثل هذه:
V = (½ x a x h) × ارتفاع المنشور
الخامس = (½ × 4 × 3) × 10
الخامس = 6 × 10
V = 60 سم 3
مساحة السطح
في حساب مساحة سطح المنشور الثلاثي ، سنستخدم صيغة مثل هذه:
L = (2 x مساحة القاعدة) + (مساحة جميع الجوانب المتعامدة)
إذا كان المثلث متساوي الأضلاع ، فيمكنك استخدام الصيغة:
L = (2 x مساحة القاعدة) + (3 x مساحة جانب واحد من العمودي)
أو يمكن أن تكون الصيغة:
L = (2 × مساحة القاعدة) + (محيط القاعدة × ارتفاع المنشور)
دعنا نلقي نظرة على مثال لهذه المشكلة لنرى كيف يتم تطبيق هذه الصيغة. فيما يلي مثال على المشكلة:
يوجد منشور مثلثي متساوي الأضلاع ارتفاعه 12 سم ، طول ضلعه 5 سم وارتفاعه 8 سم. إذن ما هي مساحة سطح هذا المنشور الثلاثي؟
المحلول:
لإيجاد مساحة السطح ، نستخدم ببساطة صيغة مساحة سطح المنشور الثلاثي كما يلي:
L = (2 x مساحة القاعدة) + (3 x من مستوى رأسي واحد)
L = (2 x (½ x 5 x 8)) + (3 x (12 x 5))
L = 40 + 180
L = 220 سم 2
هذه هي الصيغ المنشورية المثلثية المختلفة التي يجب أن تعرفها ، بالإضافة إلى بعض أمثلة المشاكل. إذا كنت لا تزال مرتبكًا ، فيمكنك أن تسأل في عمود التعليقات ، أو يمكنك تجربة Smart Class ، منصة التدريس الموثوقة عبر الإنترنت في العالم.









